Imaginez-vous dans une salle de concert. Un orchestre joue une symphonie complexe et émouvante. Chaque instrument produit sa propre mélodie, et pourtant, ensemble, ils forment une harmonie parfaite. En mathématiques, l’analyse harmonique fait exactement cela : elle décompose un phénomène complexe en notes simples, appelées « harmoniques », pour mieux comprendre comment l’ensemble fonctionne.
🌊 Qu’est-ce que l’analyse harmonique ?
L’analyse harmonique est une branche essentielle des mathématiques qui étudie comment les fonctions ou les signaux complexes peuvent être décomposés en éléments fondamentaux simples, appelés harmoniques. Ces harmoniques sont généralement représentées sous forme d’ondes sinusoïdales simples, comme des vibrations régulières ou des sons purs.
Concrètement, elle s’appuie sur l’idée que toute fonction complexe peut être représentée par une combinaison de fonctions simples, appelées ondes harmoniques, qui ressemblent à des oscillations régulières (des sinus ou cosinus, comme celles que l’on apprend au lycée).
🎵 Les harmoniques : ces briques élémentaires
Chaque phénomène périodique, comme le son d’une corde de guitare ou la lumière émise par une ampoule, peut être divisé en une série de vibrations élémentaires appelées harmoniques. Imaginez frapper une corde de guitare : elle produit une note principale (la fréquence fondamentale), mais aussi d’autres sons, plus discrets et aigus, les harmoniques, qui enrichissent son timbre.
Harmoniques et mathématiques :
- Mathématiquement, une harmonique est une fonction sinusoïdale simple, exprimée comme suit :
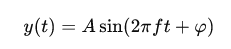
où :
- A est l’amplitude (intensité de l’onde),
- f la fréquence (hauteur du son),
- t représente le temps,
- φ est la phase (décalage temporel de l’onde).
En combinant ces harmoniques avec différentes intensités et fréquences, on peut recréer pratiquement n’importe quel phénomène périodique.
🔍 La magie de la transformée de Fourier
Au cœur de l’analyse harmonique se trouve la transformée de Fourier, un outil puissant qui permet de décomposer n’importe quel signal complexe en ses harmoniques de base. C’est comme analyser un gâteau pour connaître précisément chaque ingrédient utilisé.
Grâce à la transformée de Fourier, nous pouvons :
- Identifier les fréquences principales d’un signal sonore.
- Comprendre la composition d’images numériques.
- Filtrer les bruits indésirables d’un enregistrement audio.
🚀 Des applications concrètes partout autour de nous
Voici des exemples concrets et détaillés d’applications pratiques de l’analyse harmonique, illustrant comment elle impacte notre vie quotidienne :
🌟 Applications concrètes de l’analyse harmonique
L’analyse harmonique, grâce à sa capacité de décomposer des phénomènes complexes en combinaisons d’ondes simples, est une clé essentielle dans de nombreux domaines techniques, scientifiques et quotidiens. Voici plusieurs exemples détaillés :
🎧 1. Compression audio et traitement musical
Exemple concret : format MP3
- Lorsque vous écoutez une musique en format MP3, une analyse harmonique (via la transformée de Fourier) est utilisée pour identifier quelles fréquences sont essentielles à l’écoute.
- Les fréquences non perceptibles ou peu audibles par l’oreille humaine peuvent alors être supprimées ou comprimées, réduisant ainsi considérablement la taille du fichier audio sans grande perte de qualité perceptible.
- C’est la raison pour laquelle des milliers de chansons peuvent tenir sur votre téléphone, tout en conservant une excellente qualité sonore.
Autres exemples musicaux :
- Logiciels d’édition audio (Audacity, Adobe Audition…)
- Synthétiseurs et logiciels musicaux pour créer ou modifier des sons en studio.
📺 2. Traitement d’image et compression vidéo
Exemple concret : format JPEG
- Lorsque vous prenez une photo avec votre smartphone, celle-ci est généralement enregistrée en JPEG. Ce format utilise des principes d’analyse harmonique (transformée en cosinus discrète, dérivée de Fourier).
- L’image complexe est décomposée en harmoniques (fréquences spatiales). Les détails subtils, peu perceptibles par l’œil humain, sont compressés ou supprimés.
- Vous obtenez ainsi des fichiers légers, rapides à partager sur internet tout en gardant une qualité visuelle très élevée.
Autres exemples vidéo :
- Formats vidéo compressés (MP4, H.264, H.265…) utilisés sur Netflix, YouTube, ou encore TikTok, exploitent aussi des principes d’analyse harmonique pour diminuer la taille des vidéos.
🎤 3. Reconnaissance vocale et intelligence artificielle
Exemple concret : assistants vocaux (Siri, Alexa, Google Assistant)
- Quand vous dites : « Dis Siri, quel temps fera-t-il demain ? », votre voix est captée et transformée en un signal numérique.
- Ce signal est analysé par des algorithmes utilisant une analyse harmonique (généralement via la transformée de Fourier rapide (FFT)), afin d’isoler et identifier précisément chaque fréquence sonore composant votre voix.
- Ces fréquences analysées permettent ensuite à une Intelligence Artificielle de reconnaître les mots et d’y répondre de façon pertinente.
Autres exemples :
- Systèmes de traduction automatique
- Logiciels de transcription vocale automatique (sous-titres YouTube automatiques, applications de dictée vocale…)
🩻 4. Imagerie médicale : IRM (Imagerie par Résonance Magnétique)
Exemple concret : diagnostic médical par IRM
- Dans une IRM, on applique un champ magnétique puissant à votre corps.
- Les atomes (particulièrement ceux d’hydrogène) réagissent à ce champ magnétique, produisant des signaux électromagnétiques très faibles.
- Une analyse harmonique sophistiquée (transformée de Fourier) permet alors de transformer ces signaux bruts en images détaillées de vos organes internes, facilitant grandement les diagnostics médicaux.
Autres exemples médicaux :
- Échographie, tomographie assistée par ordinateur (scanner).
📡 5. Télécommunications : Wi-Fi et réseaux mobiles
Exemple concret : communication sans fil
- Quand vous utilisez votre téléphone portable, celui-ci communique par ondes radio avec une antenne relais.
- Ces ondes complexes, envoyant simultanément de nombreuses données, sont traitées grâce à l’analyse harmonique pour extraire l’information utile (appels, messages, connexion internet…).
- La technologie OFDM (Orthogonal Frequency-Division Multiplexing) très utilisée en 4G, 5G et Wi-Fi repose directement sur une utilisation avancée de la transformée de Fourier.
Autres exemples télécommunications :
- Radio FM, télévision numérique, Bluetooth…
🌊 6. Météorologie et étude des ondes marines
Exemple concret : prévisions météo précises
- Les stations météorologiques reçoivent des signaux émis par des satellites et capteurs terrestres.
- Une analyse harmonique de ces signaux (vents, pression atmosphérique, températures…) permet d’isoler des cycles et des motifs récurrents (comme les saisons, les oscillations climatiques).
- Grâce à cette décomposition, les météorologues peuvent mieux prévoir les événements météo avec plus de précision.
Autres exemples liés à la nature :
- Analyse des marées (variations du niveau marin), étude des tremblements de terre (sismologie).
🚀 7. Astrophysique : détection des exoplanètes
Exemple concret : identifier des planètes éloignées
- Pour détecter des exoplanètes, les astrophysiciens observent l’intensité lumineuse des étoiles très éloignées.
- De légères variations périodiques de lumière (identifiées par analyse harmonique précise) indiquent souvent la présence d’une planète passant devant son étoile (méthode dite des transits).
- L’analyse harmonique aide à identifier ces minuscules variations, quasiment imperceptibles à l’œil humain.
Autres exemples astrophysiques :
- Analyse des ondes gravitationnelles, étude des pulsars (étoiles à neutrons tournant très vite).
⚡ 8. Électricité et réseaux électriques intelligents (Smart grids)
Exemple concret : identifier des perturbations électriques
- Les fournisseurs d’électricité utilisent l’analyse harmonique pour étudier la qualité du courant électrique fourni.
- L’apparition d’harmoniques parasites indique des dysfonctionnements ou une détérioration des équipements électriques.
- Identifier ces harmoniques permet de prévenir des pannes, et d’améliorer l’efficacité énergétique.
Autres exemples liés à l’électricité :
- Détection précoce des pannes, optimisation de la distribution d’énergie.
📚 En résumé : Pourquoi c’est fascinant ?
L’analyse harmonique, en apparence abstraite, est partout autour de nous. En transformant des phénomènes complexes en composants élémentaires simples, elle nous permet de mieux comprendre, analyser et améliorer notre environnement technologique quotidien. Cette discipline mathématique est donc essentielle à des innovations pratiques variées : du téléphone que vous utilisez chaque jour, au diagnostic médical, en passant par la musique que vous écoutez et les images que vous partagez en ligne.
🌌 Vers de nouvelles frontières scientifiques
Récemment, l’analyse harmonique a même permis de résoudre de grandes conjectures mathématiques. Elle a joué un rôle crucial dans le progrès des mathématiques pures à travers le programme de Langlands, établissant des liens essentiels entre l’analyse harmonique, la théorie des nombres et d’autres domaines mathématiques. En astrophysique, elle est à l’origine de la détection révolutionnaire des ondes gravitationnelles, prédites par Einstein, permettant d’étudier précisément des événements cosmiques extrêmes comme la fusion de trous noirs. Sur le plan théorique, l’analyse harmonique s’est enrichie avec la généralisation aux structures mathématiques complexes grâce à l’analyse harmonique non commutative, qui étend les outils classiques à des contextes plus abstraits. Dans le domaine médical, des techniques telles que la microscopie de seconde harmonique profitent de ces méthodes pour obtenir des images précises de structures biologiques, facilitant ainsi le diagnostic de maladies complexes. Enfin, des mathématiciens de renom comme Terence Tao ont mis en évidence son importance profonde, notamment en prouvant le célèbre théoréme de Green-Tao et en travaillant sur la conjecture de Kakeya, soulignant comment cette discipline agit comme un puissant levier pour de nombreuses avancées scientifiques et technologiques.
En mode de conclusion : en explorant la symphonie cachée derrière les choses qui nous entourent, l’analyse harmonique continue d’ouvrir des portes vers de nouvelles découvertes passionnantes, façonnant notre manière de voir, d’écouter et de comprendre le monde.
Partager cet article:




Laisser un commentaire